Este es un pequeño glosario de artes gráficas y materias relacionadas con ellas (óptica, periodismo, tipografía, etc…). Además de un listado alfabético y de un formulario de búsqueda, se incluye un índice temático por áreas grupos de interés (PDF, Óptica, Tipografía, Preimpresión, etc…). En la medida de lo posible, se indica el equivalente en inglés, francés, italiano, alemán, catalán y portugués del término descrito.
Aviso: Este glosario está en una actualización interna importante. Durante algún tiempo algunos enlaces podrían no funcionar adecuadamente. Gracias por la paciencia.
Gustavo Sánchez Muñoz (Gusgsm), 2025
Unidad de medida tipográfica formada por la mitad de un cuadratin. En las fuentes más tradicionales solía ser el ancho de la letra "N" (versal).
En diseño gráfico, la rejilla base (baseline grid) es el conjunto de líneas horizontales imaginarias que controlan la colocación de los textos en las páginas para que se apoyen sobre ella por sus líneas base (baseline) y tengan así una apariencia ordenada y cómoda para la vista.
La rejilla base es una pauta que también se usa para apoyar otros elementos gráficos como imágenes, recuadros, rayas, etc.
El uso de las rejillas base impone una ordenación visual de ejes horizontales que facilita a los diseñadores la creación de trabajos con un acabado profesional, y a los lectores el acceso a la información contenida en esos diseños. En ese sentido cumple una misión similar a las rayas de un cuaderno pautado, que ayudan a escribir sin torcerse.
Aunque relativamente moderna, el uso de rejillas base es anterior a la autoedición y el uso del ordenador en el diseño gráfico. Los programas profesionales de diseño gráfico para documentos multipágina (como InDesign o Quark Xpress) incorporan rejillas base.
La rejilla base es una herramienta del diseñador invisible para los lectores, que nunca la ven, aunque perciban su presencia en el resultado final en forma de orden.
Por eso, en fotocomposición, las rejillas base anteriores al uso de ordenador tenían la forma de finas rayas azules dibujadas en las hojas de montaje (ya que los tonos claros de azul no se reproducía en los aparatos de fotomecánica de la época).
En los los programas informáticos de diseño gráfico, la rejilla base tampoco se imprime y se puede mostrar/ocultar y modificar en apariencia, medidas, etc.
En tipografía, el símbolo @. Aunque actualmente se usa para cosas muy diversas, su origen parece hallarse a finales de la Edad Media (si no antes) para referirse al precio de unidades de vino y grano. De ahí su habría extendido más tarde, sobre todo en el mundo anglosajón, a un significado del tipo de "el precio de cada unidad…" o "cada unidad a un precio de…"; por ejemplo: Each book @ 5.00 US dollars.
Sea cual sea su origen, su presencia en los teclados y codificaciones de ordenador ha hecho que en la actualidad se use para dos cosas (además de con ese primer sentido):
Regla de proporcionalidad que establece la proporción de los lados de un rectángulo haciendo que el lado más largo sea la suma del lado más largo y el mas corto.
Esa regla establece que el aumento o disminución de cualquier otro rectángulo se establezca manteniendo esa proporción hacia arriba o hacia abajo: El lado corto del siguiente rectángulo hacia arriba medirá lo que medía el largo del anterior, mientras que el nuevo lado largo será la suma de los lados corto y largo del rectángulo anterior.
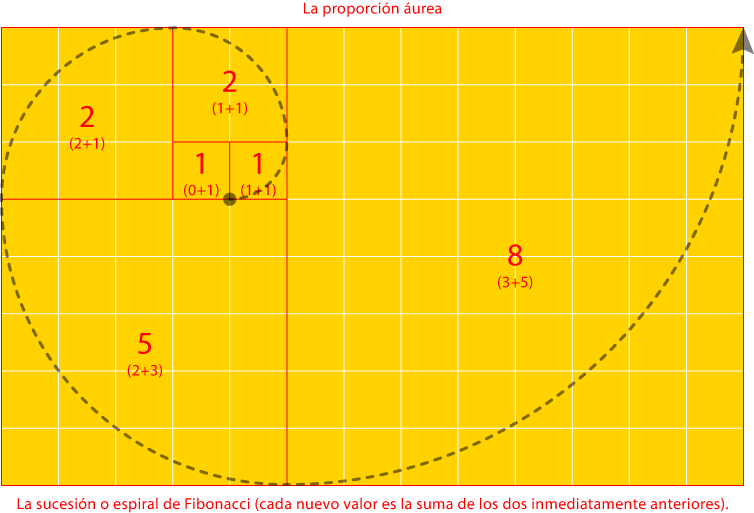
Así, por ejemplo, como un cuadrado tiene lados 1×1, el siguiente cuadrado en la proporción deberá tener 1×2, mientras que el siguiente tendrá 2×5, el siguiente rectángulo deberá tener la proporción 5×8 y así hasta el infinito.
Esta proporción subyace en muchos elementos de la naturaleza y tradicionalmente se le han atribuido propiedades divinas o místicas.
En diseño, su ventaja viene de que permite crear módulos proporcionales de forma muy sencilla y sin necesidad de cálculos, ya que se puede hacer con un simple cordel para crear un cuadrado básico que vaya aumentando al trazar un cuarto de círculo desde la esquina de cada lado más largo para obtener un nuevo lado más largo.
La relación entre ambos lados se establece a través de un número irracional llamado Phi (φ), que (muy redondeado) es 1,6180. Esa cifra se considera el número áureo.
A esta proporción también se la llama "sección áurea", o "Número áureo".
Unidad de medida de la temperatura cuyo inicio se sitúa en el cero físico absoluto (equivalente a 273 grados centígrados negativos), por lo que no tiene nunca caracter negativo, ya que es imposible.
Se usa en colorimetría y fotografía al hablar de la temperatura de color de una fuente de luz o de un iluminante.
Es "kelvin", no "grado kelvin".
